KELOMPOK 10
- DIAH WULANSARI
- IIS ARISKA
- AMIK WAHYU NINGSIH
ISOMETRI
DEFINISI
Suatu
refleksi pada garis s adalah suatu fungsi M yang didefinisikan untuk
setiap titik P pada bidang sebagai berikut.
Untuk
menyatakan refleksi garis s akan digunakan symbol Ms. Garis s
disebut sumbu refleksi. Mengingat refleksi garis bagian penting dalam geometri
, apakah fungsi juga merupakan transformasi. Untuk mengetahuinya, perlu dijawab
tiga pertanyaan tentang garis refleksi Ms , yaitu :
1 1. apakah domainnya terdiri atas semua
titik pada bidang ?
2 2. apakah setiap titik bidang pada bidang
merupakan peta ( bayangan ) beberapa
titik oleh fungsi Ms ?
3.apakah fungsi satu – satu, yaitu titik –
titik yang berbeda dipetakan onto ke bayangan ( peta ) yang berbeda ?
Jelas bahwa setiap titik dalam
bidang terletak pada s atau titik pada s.
Karena kita mempunyai aturan dalam fungsi M untuk mendapatkan peta ( bayangan )
untuk semua titik, maka domainnya pasti
termasuk semua titik pada bidang.
Hal ini memperlihatkan bahwa P adalah peta ( bayangan ) dari beberapa titik
, berarti kita bisa menyimpulkan bahwa Ms adalah pemetaan dari
bidang onto bidang. Untuk memperlihatkan Ms fungsi satu – satu akan
dilakukan bukti tak langsung da mengandaikan ada titik R dan S yang berbeda
sedemikian hingga:
 maka s adalah garis bagi yang tegak lurus
dari RK dan SK, hal ini tidak mungkin.
Sebab, tidak ada satu garis yang dapat menjadi garis bagi tegak lurus dari dua segmen
berbeda yang titik ujung segmen itu sama.
maka s adalah garis bagi yang tegak lurus
dari RK dan SK, hal ini tidak mungkin.
Sebab, tidak ada satu garis yang dapat menjadi garis bagi tegak lurus dari dua segmen
berbeda yang titik ujung segmen itu sama.
Hal
ini bertentangan dengan asumsi bahwa R dan S dua titik berbeda,. Jadi , tidak
ada titik – titik berbeda yang dipetakan onto ke titik yang sama. Akibatnya, Ms
adalah pemetaan satu – satu. Ini berarti membuktikan teorema berikut :
TEOREMA 1.1
Setiap
refleksi garis adalah transformasi. Sifat yang utama dari refleksi garis adalah
mempertahankan jarak. Maksudnya,
dalam refleksi garis, bayangan dari dua titik berbeda dipisahkan pada jarak
yang sama seperti titik – titik asalnya. Selanjutnya, suatu transformasi yang
mempunyai sifat mempertahankan jarak disebut suatu isometri.
DEFINISI
Suatu transformasi T adalah isometri jika dan hanya jika
untuk setiap pasangan titik – titik P dan Q,
Bukti ,
Pembuktiannya menggunakan koordinat geometri. Kita ingat
bahwa sautu sistem koordinat dapat dibentuk dengan menggunakan sepasang garis
tegak lurus dalam satuan panjang, serta menetapkan sumbu x dan y positif, kita
bebas memilih sumbu mana yang akan dijadikan sumbu refleksi. Dalam hal ini,
dipilih sumbu x sebagai garis s nya, sedangkan sumbu y menjadi garis
tegak lurus s.
SIFAT – SIFAT
PENJUMLAHAN ISOMETRIS
Seperti dijelaskan terdahulu, refkeksi garis mempunyai
sifat – sifat dasar, yaitu :
1. 1.
Pemetaan satu – satu dari bidang onto
bidang
2. 2.
mempertahankan jarak
Sifat
– sifat di atas telah kita ketahui gambarannya tentang bayangan ( peta ) tidak
satu per satu melalui suatu transformasi. Bagaimana halnya dengan transformasi
sekelompok titik ? Misalnya, apa yang terjadi dengan transformasi suatu
segitiga oleh refleksi sumbu y ? Seperti
yang sudah dibicarakan sebelumnya tentang notasi transformasi suatu titik, maka
notasi itu dapat kita perluas pula untuk menyatakan transformasi dan fungsi
sekelompok titik.
1.Pencerminan garis memetakan garis lurus onto
garis lurus
2.Pencerminan garis mempertahankan ukuran sudut
antara garis – garis
3.Pencerminan garis mempertahankan kesejajaran dan
ketegaklurusan garis – garis
Contoh bahwa garis
mempertahankan kesejajaran, jika dua garis sejajar, mmaka bayangan ( Peta )
juga sejajar.
Menurut definisi , suatu isometric adalah pemetaan satu –
satu yang mempertahankan jarak dari bidang onto bidang. Sifat – sifat 3, 4, 5 dapat
dibuktikan untuk suatu issometri. Karena refleksi garis tidak hanya sifat 3,4,
dan 5, generalisasi yang lebih luas,
yaitu mengansumsikan bahwa suatu T hanya mempunyai sifat mempertahankan jarak. Apabila, selanjutkan
ditunjukkan bahwa T mempunyai sifat – sifat itu, maka kita telah membuktikan
bahwa setiap isometri mempunyai sifat – sifat itu juga. Karena pencerminan
garis adalah isometric., maka sifat – sifat berlaku secara khusus pada refleksi
garis.
Logika pembuktian
seperti di atas akan menolong kita ketika menguji suatu jenis transformasi yang
baru, sehingga cukuplah ditunjukkan bahwa pemetaannya mempertahankan jarak ,
yaitu :
·
yang memetakan garis onto garis
·
yang mempertahankan ukuran sudut,
kesejajaran , dan ketegaklurusan
Karena preservasi ukuran sudut, kesejajaran,
dan ketegaklurusan antargaris bergantung
pada fakta bahwa bayangan ( peta )
suatu garis pastilah garis, maka kita mulai dengan pembuktian isometric
memetakkan garis onto garis.
COROLLARY
Bayangan dua garis oelh
suatu isometric adalah tegak lurus jika dan hanya jika garis – garis semula itu
tegak lurus.
TEOREMA
Bayangan
( peta ) dua garis oleh suatu isometric adalah sejajar jika dan hanya jika
garis – garis semula itu sejajar.
ISOMETRI YANG
LANGSUNGDAN BERLAWANAN
Menurut pembicaraan dalam sub bab terdahulu, ismoetri
memiliki sifat mempertahankan ukuran panjang antara segmen – segmen dan ukuran
sudut antarsegmen, seolah – olah kita memiliki alat pengerak/ pemindah yang
membawa suatu objek tanpa merussak apalagi mengubah bentuk objek tersebut.
Pada dasarnya , terdapat dua jenis isometric. Pertama ,
yang memindahkan bangun geometri langsung dari satu posisi ke posisi lain. Kedua,
yang memindahkan suatu bangun dengan memutar bangun tersebut.
Sejauh ini, perbedaan mendasar antarisometri mungkin
belum jelas. Karena itu, berikut ini akan diberikan gambaran secara matematis
yang lebih tepat lagi tentang isometric. Pertama akan dikenalkan pad aide
tentang orientasi suatu urutan tiga titik yang tak segaris.
Jika ( P1P2P3) adalah
tiga titik berurutan yang tak segaris, maka dengan tepat ada sebuah lingkaran b
yang melalui P1P2 dan P3. Dimulai dari P1,
kita dapat bergerak melingkari b sehingga bertemu P2 dan selanjutnya
P3 dan akhirnya kembali P1. Jika arah keliling ini titik
( P1P2P3) memiliki orientasi yang sesuai
dengan arah putaran jarum jam. Apabila arah keliling itu berlawanan dengan arah
putaran jarum jam, maka dikatakan bahwa tiga titik ( P1P2P3)
memiliki orientasi yang berlawanan dengan arah jarum jam.
Suatu transformasi membalikkan orientasi jika untuk
setiap tiga titik yang tidak segaris orientasinya tidak sama dengan orientasi
peta – petanya. Suatu pemetaan disebut pemetaan itu membalikkan orientasi.
POSTULAT
Setiap refleksi garis
adalah suatu ismometri berlawanan satu dari isometric adalah jika isometric itu
membalikkan sebuah tiga titik berurutan, maka isometric itu membalikkan setiap
tiga titik, dan jika isometric itu mengawetkan sebuah orientasi tiga buah
titik, maka isometric itu mengawetkan setiap orientasi tiga titik.
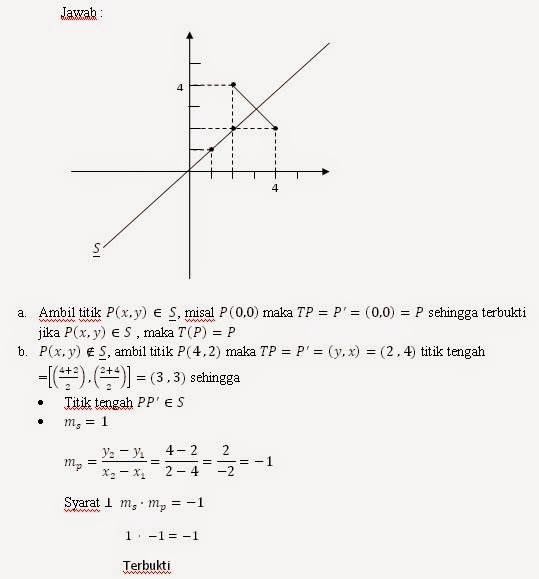
LATIHAN SOAL DAN PEMBAHASAN

















suka. uraiannya bisa dicerna
BalasHapusSumber bukunya ???
BalasHapus